この記事はこんな人向けです。
・FIREまでの年数が長くてうんざりしている
・貯蓄率が大事なのはわかっているけど、もっと細かくFIREまでの年数を計算したい
サイドFIREまでの年数が知りたい
前回の記事では、貯蓄率からFIREまでの年数を計算してみました。
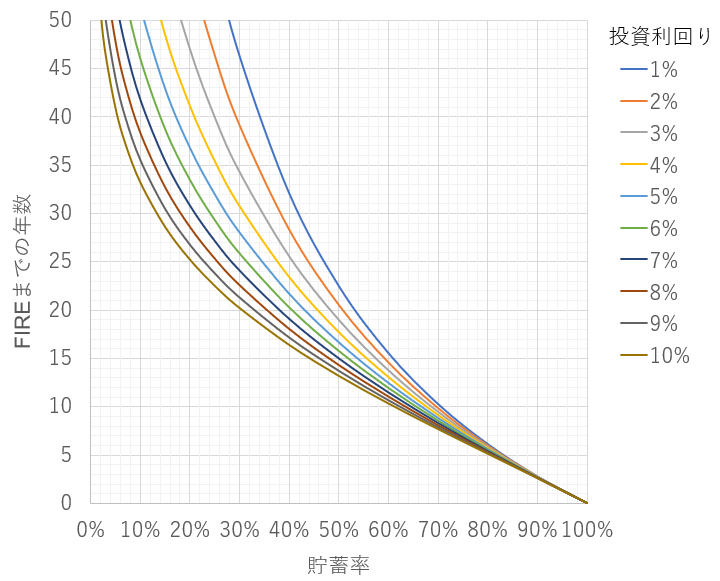

貯蓄率25%とかだとFIREに30年以上かかるのは絶望、、、

上のグラフだと、初期資産0円かつ完全FIREだからね。
サイドFIREならもっと短くなるかも?
現資産でサイドFIREするまでの年数は?
上記を踏まえた上で、FIREするまでの年数計算ツール、サイドFIRE Ver.を作成してみました。
ぜひ色々なパターンで計算してみてください。
※前提条件:年収×0.8=手取り、年間投資利回り5%
年収(税引前)[単位:万円]:
年間支出[単位:万円]:
現在の資産[単位:万円]:
リタイア後の手取月収(サイドFIREの場合入力)[単位:万円]:
手取り概算: 万円
年間支出: 万円
年間貯蓄額: 万円
貯蓄率:
FIRE時に必要な資産額: 万円
FIRE・サイドFIREまでの年数: 年
ちなみに我が家の現在の条件で計算すると以下のようになりました。
(現資産3,750万円)
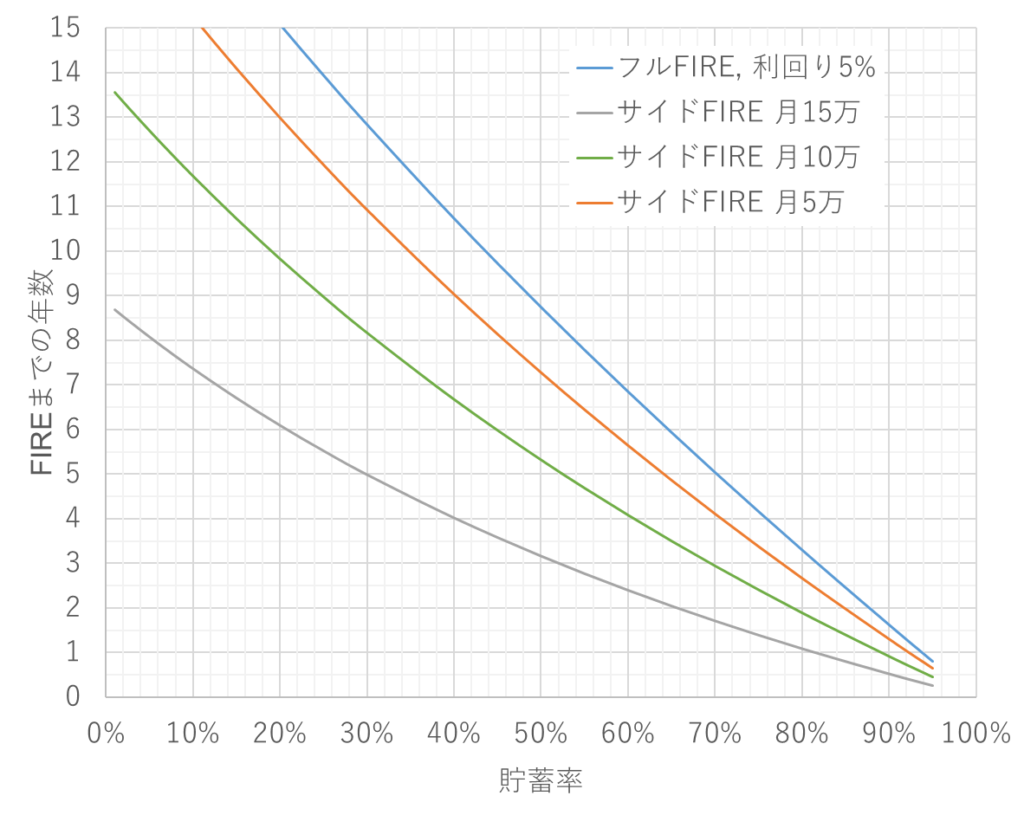

例えば貯蓄率60%を維持できれば、約4年で月10万のサイドFIREできそう!
これなら頑張れるかも?

何事も①理想と現実のギャップを知る②実現可能な目標を立てる
このステップが重要だね。
詳しい計算方法について解説

ここではフルFIREの計算式も含めて、FIREの計算式を解説します。
興味ない方は読み飛ばしてくださいね。
(フルFIRE想定)
資産の4%で支出を賄うので、
\(資産\times0.04=年間支出\)
この式から各種条件のもと式変形していきます。
資産と年間貯蓄額Sの関係性は、利回りR(=1+r)によって年々増加するので、
※利回り5%ならR=1.05, r=0.05とする。
1年目:\(資産=S\)
2年目:\(資産=SR+S\)
3年目:\(資産=SR^2+SR+S\)
・・・
N年目:\(資産=SR^{(N-1)}+SR^{(N-2)}+\cdots+S\)
\(=S\times(R^{(N-1)}+R^{(N-2)}+\cdots+1)\)
これは初項S、等比Rの等比数列になるので、等比数列の和の公式を用いて、
\(\displaystyle 資産=S\times\frac{1-R^N}{1-R}=S\times\frac{1-R^N}{-r}\)
これを元の式にいれると、
\(\displaystyle S\times\frac{1-R^N}{-r}\times0.04=年間支出\)
\(\displaystyle R^N=\frac{r}{0.04}\frac{年間支出}{S}+1\)
ここで年間支出と年間貯蓄Sの関係性は、両者を年間収入で割れば貯蓄率tで表すことができます。
\(\displaystyle \frac{年間支出}{年間貯蓄S}=\frac{\frac{年間支出}{年間収入}}{\frac{年間収入-年間支出}{年間収入}}=\frac{1-t}{t}\)
したがって、
\(\displaystyle R^N=\frac{r}{0.04}\frac{1-t}{t}+1\)
\(\displaystyle N=\log{R}\left(\frac{r}{0.04}\frac{1-t}{t}+1\right)\)

高校数学くらいの知識で解けるね!
(サイドFIREの場合)
上の式に、初期資産額\(S_0\)を加えます。
N年目:\(資産=S_0^{(N-1)}+S\times(R^{(N-1)}+R^{(N-2)}+\cdots+1)\)
\(\displaystyle =S_0 R^{(N-1)}+S\times\frac{1-R^N}{-r}\)
\(\displaystyle =R^N\left(\frac{S_0}{R}+\frac{S}{r}\right)-\frac{S}{r}\)
年間支出EからサイドFIRE後の年収\(I_0\)引いて、
\(\displaystyle R^N\left(\frac{S_0}{R}+\frac{S}{r}\right)-\frac{S}{r}=\frac{(E-I_0)}{0.04}\)
\(\displaystyle R^N\left(\frac{S_0}{R}+\frac{S}{r}\right)=\frac{(E-I_0)}{0.04}+\frac{S}{r}\)
したがって、
\(\displaystyle R^N=\frac{\frac{(E-I_0)}{0.04}+\frac{S}{r}}{\frac{S_0}{R}+\frac{S}{r}}\)
\(\displaystyle N=\log{R}\left(\frac{\frac{(E-I_0)}{0.04}+\frac{S}{r}}{\frac{S_0}{R}+\frac{S}{r}}\right)\)

正直わけがわからん、、、
まとめ:目指せFIREならぬサイドFIRE!
今回は現在の資産も含めたサイドFIREまでの年数を計算してみました。
フルFIREと比べるとかなり年数が短くできることが実感できましたね。

みなさんも計算してみてね!
ではまた🐼



コメント